Bini's Unterrichtsmaterial -

Schularbeitsvorbereitung

In manchen Browsern werden Formeln leider (noch) nicht korrekt angezeigt. Ein Klick auf die unschöne Darstellung führt zu einem Bild der Formel.

Bruchterm vereinfachen

Vereinfache durch Herausheben und überprüfe mittels geigneter Probe:

$\frac{4 a^{3} - 8 a^{2}}{12 a^{5}} =$

Lösung

Bruchtreme

Vereinfache und berechne:

$\frac{a - 3 b}{4 a - 2 b} : \frac{a^{2} - 9 b^{2}}{3 b - 6 a} =$

Welche Bedingungen müssen für die Variablen erfüllt sein?

Bruchtreme

Vereinfache und berechne:

$\frac{3 x - 6 y}{9 x^{2}} : \frac{4 y - 2 x}{3 x + y} =$

Welche Bedingungen müssen für die Variablen erfüllt sein?

Bruchtreme

Für welche reellen Zahlen ist der folgende Term definiert?

$T (a) = \frac{2 a^{2} - 5 a + 13}{3 a - 7}$

Bruchtreme

Für welche reellen Zahlen ist der folgende Term definiert?

$T (x) = \frac{3 x^{2} - 7 x + 15}{9 - 4 x}$

Bruchtreme

Vereinfache den angegebenen Term. Bestimme die Definitionsmenge bezüglich Q und führe die Probe mit s=1 durch.

$T (s) = \frac{2 s}{s - 3} - \frac{5 s^{2} - 45}{s^{2} - 9} - \frac{3 s}{3 - s}$

Lösung

Bruchtreme

Vereinfache den angegebenen Term. Bestimme die Definitionsmenge bezüglich Q und führe die Probe mit a=1, b=2 durch.

$T (a, b) = \frac{\frac{a^{2} + b^{2}}{6 a b} - \frac{1}{3}}{\frac{a - a^{2} - b}{a b} + \frac{a}{b}} \cdot \frac{2 a}{a - b}$

Lösung

Deltoid

Konstruiere ein Deltoid e= 7,5 cm, f = 6,6 cm, γ = 90° und berechne den Flächeninhalt!

Dreiecksberechnung

Von einem rechtwinkeligen Dreieck kennt man a=38,3cm und h_c=23,9cm.
Fertige eine übersichtliche Skizze an und berechne b, c, p, q, A!

Dreiecksberechnung

Von einem allgemeinen Dreieck kennt man die Längen von a=12cm, h_a=7cm, c=14cm. Berechne die Länge der Höhe h_c!

Lösung

Dreiecksberechnung

Von einem allgemeinen Dreieck kennt man die Längen von b=45mm, h_c=30mm, c=64mm. Berechne die Länge der Höhe h_b!

Lösung

Ein seltsames Flugobjekt

Ein Drache in klassischer Form hat eine Fläche von 13750cm² und eine Spannweite von 450cm. Berechne die Länge der zweiten Achse! Fertige eine Skizze an! Warum wird dieses Gebilde nicht gut steigen?

Lösung

Grundstücksskauf

Frau Clever kauft das Grundstück A, Frau Einfalt das Grundstück B laut Skizze. Beide bezahlen € 23.200,-
Wer von beiden hat günstiger gekauft? Welches Grundstück würdest du kaufen? Beründe deine Antwort!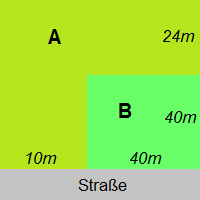

Abbildung

Lösung

Grundstücksspekulation

Herr Müller erwirbt ein rechteckiges Grundstück (a=50m, b=35m) und bezahlt dafür EUR 21.875,-
Wegen eines Straßenbauvorhabens muss er eine Ecke jeweils 10m von der ursprünglichen Ecke aus gemessen abgeben und erhält dafür EUR 600,-
Hat Herr Müller ein gutes Geschäft gemacht? Begründe die Antwort durch eine Gewinn-/Verlustrechnung!

Lösung

Grungdstücksteilung

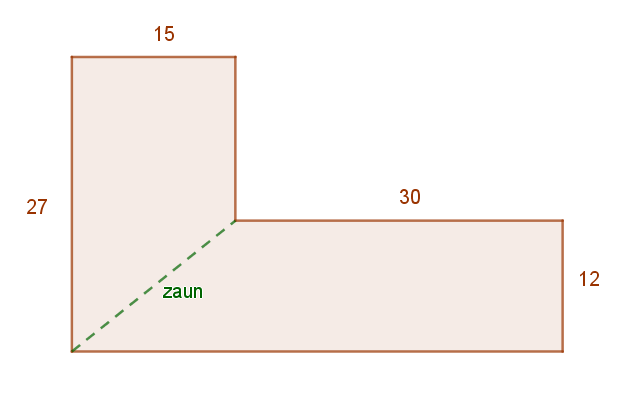
Ein L-förmiges Grundstück soll, wie in der Skizze angegeben, durch einen Zaun geteilt werden. Berechne die Länge des Zaunes und die Größe der beiden Teilflächen!

Abbildung

Leiter

Eine Leiter l=6m wird an eine Hauswand gelehnt, so dass die Standfüße in einem Abstand von a=1,5m zur Hauswand bilden.
Berechne in welcher Höhe h die Leiter die Wand berührt!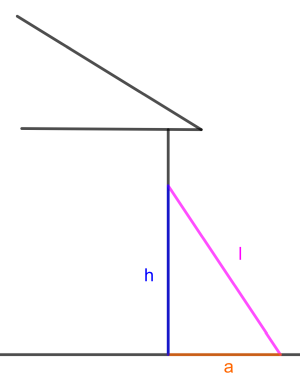

Abbildung

Lösung

Limonade

In der Limonadenfabrik sollen 3000 Flaschen befüllt werden. Drei Maschinen schaffen dies in 48 Minuten.

Erstelle ein Tabelle mit den Füllzeiten, wenn 2, 4, 7 Maschinen zum Einsatz kommen.
Erstelle ein Diagramm, das diesen Zusammenhang darstellt.
Bestimme die Art der Proportion und berechne den Proportionalitätsfaktor.

Lösung

Parallelogramm

Von einem Parallelogramm kennt man a=7cm, b=5cm und h_a=4cm. Berechne die Länge der Höhe auf b und überprüfe durch eine Konstruktion!

Lösung

Radwanderung

Johanna unternimmt eine mehrtäge Radtour. Am ersten Tag fährt sie 5 Stunden und legt dabei 75km zurück, am zweiten Tag schafft sie 90km, wobei sie Vormittag und Nachmittag je drei Stunden unterwegs ist. Am letzten Tag fährt sie nur mehr eine kurze Strecke von 40km und braucht dafür 2 Stunden.
Stelle fest, ob die Fahrzeit zur Weglänge proportional ist und begünde die Antwort.

Lösung

Raute

Konstruiere eine Raute a=5cm, e=8cm und berechne den Flächeninhalt!

Lösung

Raute

Konstruiere eine Raute a = 5,6 cm, β = 105° (o.W.) und berechne den Flächeninhalt (mit Maßen aus der Konstruktion)!

Raute

Konstruiere eine Raute a = 5,6 cm, β = 105° (o.W.) und berechne den Flächeninhalt (mit Maßen aus der Konstruktion)!